Homework 1

Rents in San Francisco 2000-2018
Kate Pennington created a panel of historic Craigslist rents by scraping posts archived by the Wayback Machine. You can read more about her work here
In our case, we have a clean(ish) dataset with about 200K rows that correspond to Craigslist listings for renting properties in the greater SF area. The data dictionary is as follows
| variable | class | description |
|---|---|---|
| post_id | character | Unique ID |
| date | double | date |
| year | double | year |
| nhood | character | neighborhood |
| city | character | city |
| county | character | county |
| price | double | price in USD |
| beds | double | n of beds |
| baths | double | n of baths |
| sqft | double | square feet of rental |
| room_in_apt | double | room in apartment |
| address | character | address |
| lat | double | latitude |
| lon | double | longitude |
| title | character | title of listing |
| descr | character | description |
| details | character | additional details |
The dataset was used in a recent tidyTuesday project.
# download directly off tidytuesdaygithub repo
rent <- readr::read_csv('https://raw.githubusercontent.com/rfordatascience/tidytuesday/master/data/2022/2022-07-05/rent.csv')What are the variable types? Do they all correspond to what they really are? Which variables have most missing values?
There are two variable types - character and numeric. Date column should be of the date data type but it is double. descr has the most missing values.
skimr::skim(rent)| Name | rent |
| Number of rows | 200796 |
| Number of columns | 17 |
| _______________________ | |
| Column type frequency: | |
| character | 8 |
| numeric | 9 |
| ________________________ | |
| Group variables | None |
Variable type: character
| skim_variable | n_missing | complete_rate | min | max | empty | n_unique | whitespace |
|---|---|---|---|---|---|---|---|
| post_id | 0 | 1.00 | 9 | 14 | 0 | 200796 | 0 |
| nhood | 0 | 1.00 | 4 | 43 | 0 | 167 | 0 |
| city | 0 | 1.00 | 5 | 19 | 0 | 104 | 0 |
| county | 1394 | 0.99 | 4 | 13 | 0 | 10 | 0 |
| address | 196888 | 0.02 | 1 | 38 | 0 | 2869 | 0 |
| title | 2517 | 0.99 | 2 | 298 | 0 | 184961 | 0 |
| descr | 197542 | 0.02 | 13 | 16975 | 0 | 3025 | 0 |
| details | 192780 | 0.04 | 4 | 595 | 0 | 7667 | 0 |
Variable type: numeric
| skim_variable | n_missing | complete_rate | mean | sd | p0 | p25 | p50 | p75 | p100 | hist |
|---|---|---|---|---|---|---|---|---|---|---|
| date | 0 | 1.00 | 2.01e+07 | 44694.07 | 2.00e+07 | 2.01e+07 | 2.01e+07 | 2.01e+07 | 2.02e+07 | ▁▇▁▆▃ |
| year | 0 | 1.00 | 2.01e+03 | 4.48 | 2.00e+03 | 2.00e+03 | 2.01e+03 | 2.01e+03 | 2.02e+03 | ▁▇▁▆▃ |
| price | 0 | 1.00 | 2.14e+03 | 1427.75 | 2.20e+02 | 1.30e+03 | 1.80e+03 | 2.50e+03 | 4.00e+04 | ▇▁▁▁▁ |
| beds | 6608 | 0.97 | 1.89e+00 | 1.08 | 0.00e+00 | 1.00e+00 | 2.00e+00 | 3.00e+00 | 1.20e+01 | ▇▂▁▁▁ |
| baths | 158121 | 0.21 | 1.68e+00 | 0.69 | 1.00e+00 | 1.00e+00 | 2.00e+00 | 2.00e+00 | 8.00e+00 | ▇▁▁▁▁ |
| sqft | 136117 | 0.32 | 1.20e+03 | 5000.22 | 8.00e+01 | 7.50e+02 | 1.00e+03 | 1.36e+03 | 9.00e+05 | ▇▁▁▁▁ |
| room_in_apt | 0 | 1.00 | 0.00e+00 | 0.04 | 0.00e+00 | 0.00e+00 | 0.00e+00 | 0.00e+00 | 1.00e+00 | ▇▁▁▁▁ |
| lat | 193145 | 0.04 | 3.77e+01 | 0.35 | 3.36e+01 | 3.74e+01 | 3.78e+01 | 3.78e+01 | 4.04e+01 | ▁▁▅▇▁ |
| lon | 196484 | 0.02 | -1.22e+02 | 0.78 | -1.23e+02 | -1.22e+02 | -1.22e+02 | -1.22e+02 | -7.42e+01 | ▇▁▁▁▁ |
Make a plot that shows the top 20 cities in terms of % of classifieds between 2000-2018.
rent %>%
group_by(city) %>%
summarize(city_count = count(city)) %>%
mutate(percent_city = city_count/sum(city_count))%>%
slice_max(order_by = percent_city,n=20) %>% #derived the top 20
ggplot(
aes(
x=percent_city,
y=fct_reorder(city,percent_city) #reordered city based on % of listings
)
) +
geom_col() +
scale_x_continuous(labels = scales::percent_format(),) +
labs(
title="San Francisco accounts for more than a quarter of all rental classifieds",
caption = "Source: Penninaton, Kate (2018). Bay Area Craigslist Rental Housing Posts, 2000-2018",
subtitle = "% of Craigslist listings, 2000-2018",
x = NULL,
y = NULL) +
theme_bw(base_size = 14)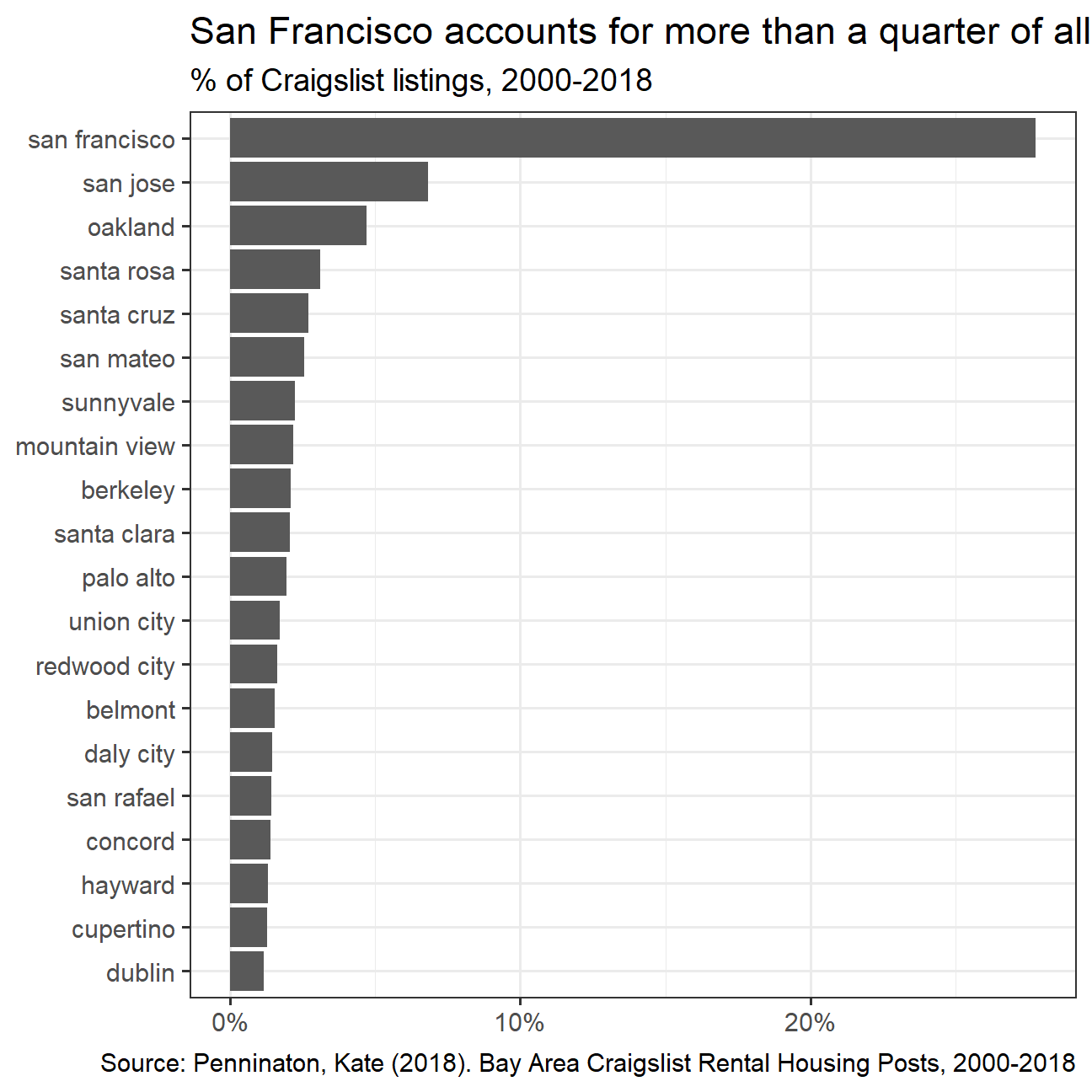
Make a plot that shows the evolution of median prices in San Francisco for 0, 1, 2, and 3 bedrooms listings.
rent %>%
filter(city=="san francisco",beds<=3) %>%
group_by(beds,year) %>%
summarize(median_price=median(price)) %>%
ggplot(aes(x=year,y=median_price,color=factor(beds))) + #setting colour for no. of beds
geom_line() +
facet_wrap(~beds,ncol=4) + #ncol is used to display the graphs in one line
labs(
title = "San Francisco rents have been been steadily increasing",
subtitle = "0 to 3-bed listings, 2000-2018",
caption = "Source: Pennington, Kate (2018). Bay Area Craigslist Rental Housing Posts, 2000-2018",
x = NULL,
y = NULL) +
theme_bw(base_size = 14) +
theme(legend.position = "none") # to remove the legend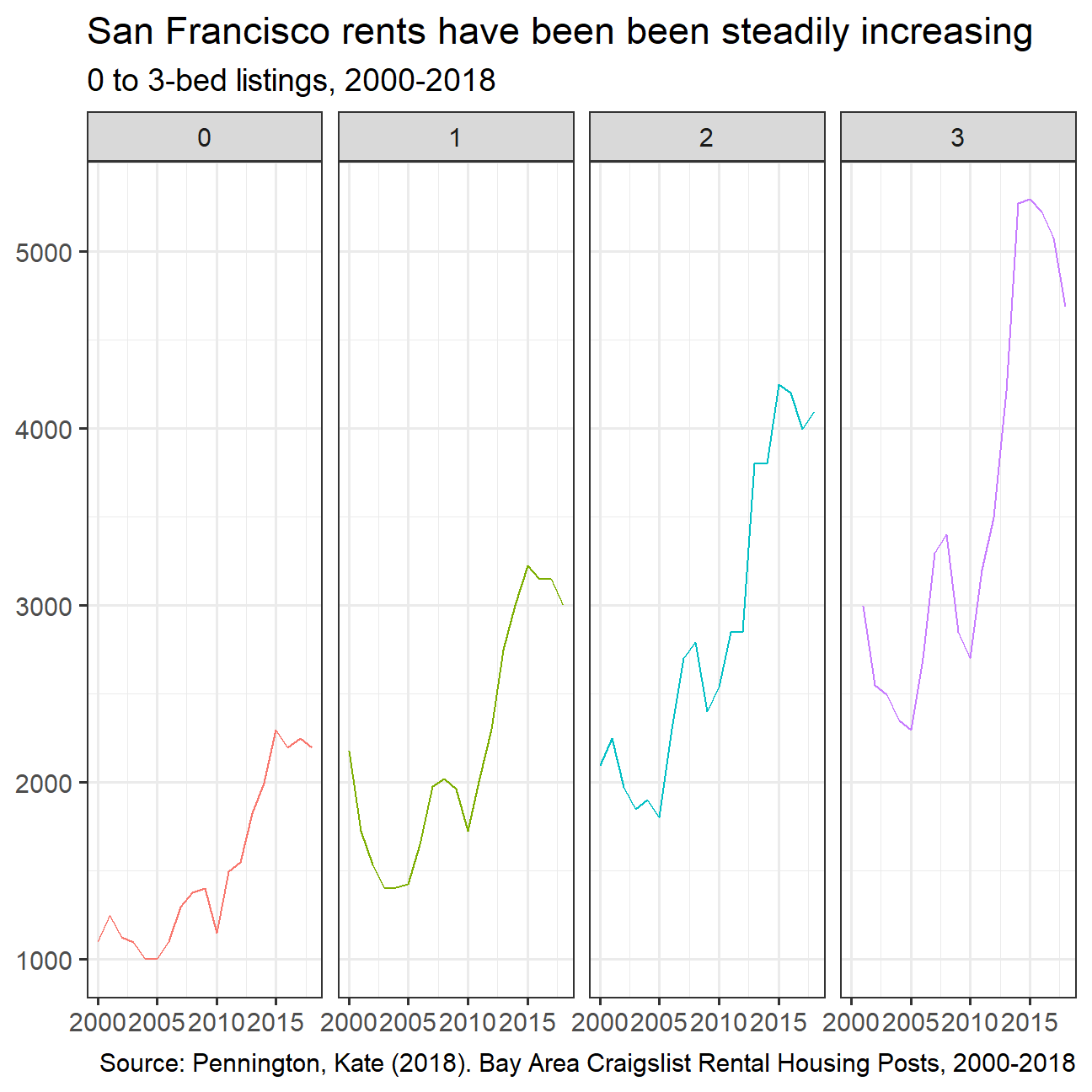
Finally, make a plot that shows median rental prices for the top 2 cities in the Bay area.
top <- rent %>%
count(city) %>%
slice_max(order_by = n, n=12) #derive the top 12 cities
vec <- c(top) #creating a vector of the top 12 cities
rent %>%
filter(city == vec$city, beds==1) %>% #filtering the cities in the vector
group_by(year, city) %>%
summarise(median_price = median(price)) %>%
ggplot(
top,
mapping=aes(x=year, y=median_price, colour = factor(city))) +
geom_line() +
facet_wrap(~city) +
labs(
title = "Rental prices for 1-bedroom flats in the Bay Area",
caption = "Source: Pennington, Kate (2018). Bay Area Craigslist Rental Housing Posts, 2000-2018",
x = NULL,
y = NULL
) +
theme_bw(base_size = 14) +
theme(legend.position = "none") 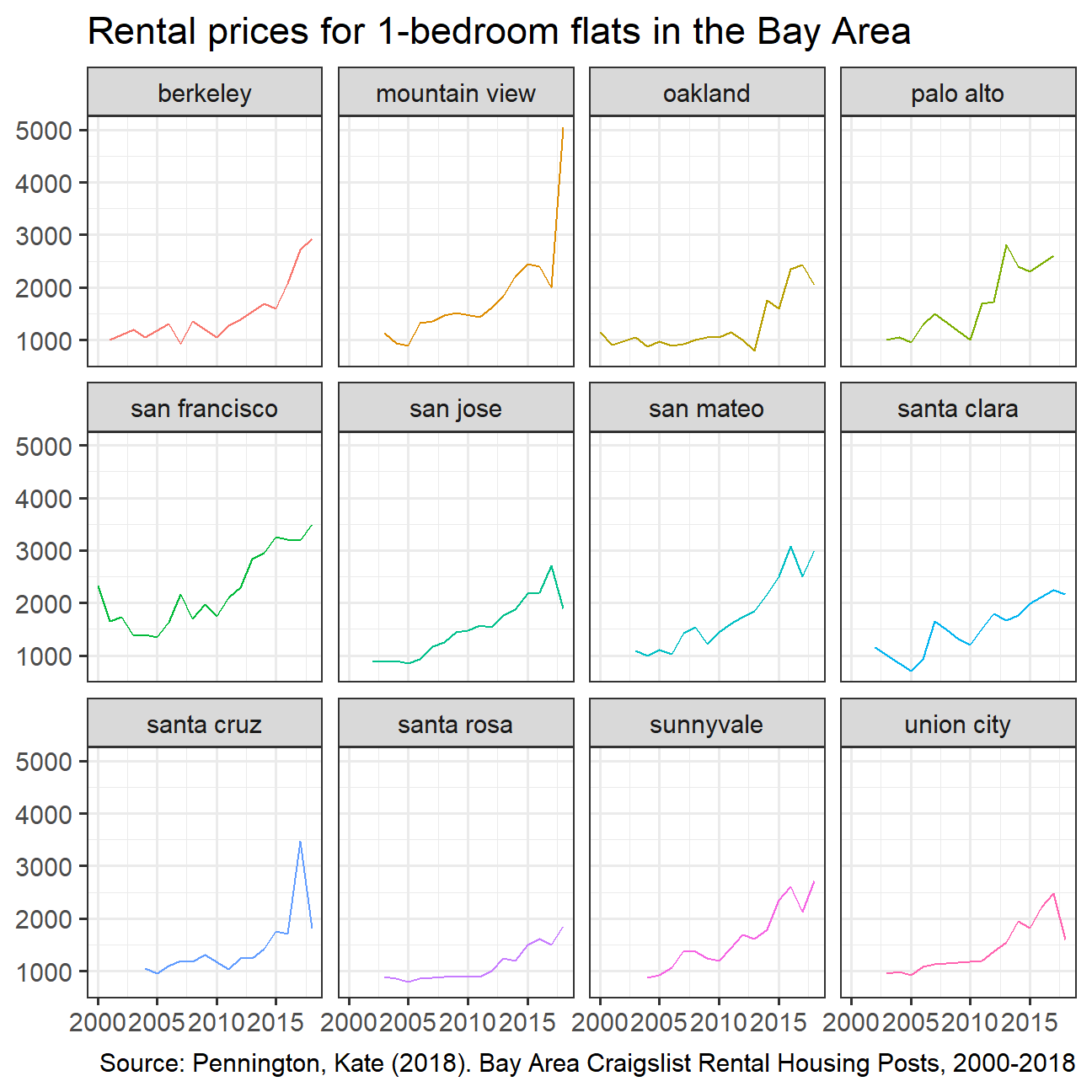
What can you infer from these plots?
When looking at the rental prices for 1 bedroom apartments in the Bay Area, we see a clear trend for all the locations. There is a clear rise in rental prices over a period of almost 20 years (2000-2018), with certain areas seeing a larger increase than others, but most areas seeing the rent prices double. Interestingly, it seems as if major social and economic events are reflected in the rental prices. For example, there was a small dip in rental prices around 2002. This is most likely because of the dot com crash that occurred two years before, which significantly impacted Silicon Valley and the Bay Area.
Similarly, a large drop can be noted around 2010 which is most likely because the continued negative effects of the financial crisis. Lastly, for some areas, with Palo Alto leading the way, we can see a sharp drop around 2015. There are no obvious external factors that can explain this drop and there for we could speculate that the large rise in prices the years before were brought back down with a correction.
Analysis of movies- IMDB dataset
We will look at a subset sample of movies, taken from the Kaggle IMDB 5000 movie dataset
movies <- read_csv(here::here("data", "movies.csv"))
glimpse(movies)## Rows: 2,961
## Columns: 11
## $ title <chr> "Avatar", "Titanic", "Jurassic World", "The Avenge…
## $ genre <chr> "Action", "Drama", "Action", "Action", "Action", "…
## $ director <chr> "James Cameron", "James Cameron", "Colin Trevorrow…
## $ year <dbl> 2009, 1997, 2015, 2012, 2008, 1999, 1977, 2015, 20…
## $ duration <dbl> 178, 194, 124, 173, 152, 136, 125, 141, 164, 93, 1…
## $ gross <dbl> 7.61e+08, 6.59e+08, 6.52e+08, 6.23e+08, 5.33e+08, …
## $ budget <dbl> 2.37e+08, 2.00e+08, 1.50e+08, 2.20e+08, 1.85e+08, …
## $ cast_facebook_likes <dbl> 4834, 45223, 8458, 87697, 57802, 37723, 13485, 920…
## $ votes <dbl> 886204, 793059, 418214, 995415, 1676169, 534658, 9…
## $ reviews <dbl> 3777, 2843, 1934, 2425, 5312, 3917, 1752, 1752, 35…
## $ rating <dbl> 7.9, 7.7, 7.0, 8.1, 9.0, 6.5, 8.7, 7.5, 8.5, 7.2, …Besides the obvious variables of title, genre, director, year, and duration, the rest of the variables are as follows:
gross: The gross earnings in the US box office, not adjusted for inflationbudget: The movie’s budgetcast_facebook_likes: the number of facebook likes cast memebrs receivedvotes: the number of people who voted for (or rated) the movie in IMDBreviews: the number of reviews for that movierating: IMDB average rating
Use your data import, inspection, and cleaning skills to answer the following:
- Are there any missing values (NAs)? Are all entries distinct or are there duplicate entries?
No there are no missing values or duplicate entries under any of the columns.
skimr::skim(movies)| Name | movies |
| Number of rows | 2961 |
| Number of columns | 11 |
| _______________________ | |
| Column type frequency: | |
| character | 3 |
| numeric | 8 |
| ________________________ | |
| Group variables | None |
Variable type: character
| skim_variable | n_missing | complete_rate | min | max | empty | n_unique | whitespace |
|---|---|---|---|---|---|---|---|
| title | 0 | 1 | 1 | 83 | 0 | 2907 | 0 |
| genre | 0 | 1 | 5 | 11 | 0 | 17 | 0 |
| director | 0 | 1 | 3 | 32 | 0 | 1366 | 0 |
Variable type: numeric
| skim_variable | n_missing | complete_rate | mean | sd | p0 | p25 | p50 | p75 | p100 | hist |
|---|---|---|---|---|---|---|---|---|---|---|
| year | 0 | 1 | 2.00e+03 | 9.95e+00 | 1920.0 | 2.00e+03 | 2.00e+03 | 2.01e+03 | 2.02e+03 | ▁▁▁▂▇ |
| duration | 0 | 1 | 1.10e+02 | 2.22e+01 | 37.0 | 9.50e+01 | 1.06e+02 | 1.19e+02 | 3.30e+02 | ▃▇▁▁▁ |
| gross | 0 | 1 | 5.81e+07 | 7.25e+07 | 703.0 | 1.23e+07 | 3.47e+07 | 7.56e+07 | 7.61e+08 | ▇▁▁▁▁ |
| budget | 0 | 1 | 4.06e+07 | 4.37e+07 | 218.0 | 1.10e+07 | 2.60e+07 | 5.50e+07 | 3.00e+08 | ▇▂▁▁▁ |
| cast_facebook_likes | 0 | 1 | 1.24e+04 | 2.05e+04 | 0.0 | 2.24e+03 | 4.60e+03 | 1.69e+04 | 6.57e+05 | ▇▁▁▁▁ |
| votes | 0 | 1 | 1.09e+05 | 1.58e+05 | 5.0 | 1.99e+04 | 5.57e+04 | 1.33e+05 | 1.69e+06 | ▇▁▁▁▁ |
| reviews | 0 | 1 | 5.03e+02 | 4.94e+02 | 2.0 | 1.99e+02 | 3.64e+02 | 6.31e+02 | 5.31e+03 | ▇▁▁▁▁ |
| rating | 0 | 1 | 6.39e+00 | 1.05e+00 | 1.6 | 5.80e+00 | 6.50e+00 | 7.10e+00 | 9.30e+00 | ▁▁▆▇▁ |
unique(movies) #find unique records in the data set## # A tibble: 2,961 × 11
## title genre direc…¹ year durat…² gross budget cast_…³ votes reviews rating
## <chr> <chr> <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 Avat… Acti… James … 2009 178 7.61e8 2.37e8 4834 8.86e5 3777 7.9
## 2 Tita… Drama James … 1997 194 6.59e8 2 e8 45223 7.93e5 2843 7.7
## 3 Jura… Acti… Colin … 2015 124 6.52e8 1.5 e8 8458 4.18e5 1934 7
## 4 The … Acti… Joss W… 2012 173 6.23e8 2.2 e8 87697 9.95e5 2425 8.1
## 5 The … Acti… Christ… 2008 152 5.33e8 1.85e8 57802 1.68e6 5312 9
## 6 Star… Acti… George… 1999 136 4.75e8 1.15e8 37723 5.35e5 3917 6.5
## 7 Star… Acti… George… 1977 125 4.61e8 1.1 e7 13485 9.11e5 1752 8.7
## 8 Aven… Acti… Joss W… 2015 141 4.59e8 2.5 e8 92000 4.63e5 1752 7.5
## 9 The … Acti… Christ… 2012 164 4.48e8 2.5 e8 106759 1.14e6 3514 8.5
## 10 Shre… Adve… Andrew… 2004 93 4.36e8 1.5 e8 1148 3.15e5 688 7.2
## # … with 2,951 more rows, and abbreviated variable names ¹director, ²duration,
## # ³cast_facebook_likes- Produce a table with the count of movies by genre, ranked in descending order
movies %>%
count(genre) %>%
arrange(desc(n)) #sort the genres in descending order on the basis of count## # A tibble: 17 × 2
## genre n
## <chr> <int>
## 1 Comedy 848
## 2 Action 738
## 3 Drama 498
## 4 Adventure 288
## 5 Crime 202
## 6 Biography 135
## 7 Horror 131
## 8 Animation 35
## 9 Fantasy 28
## 10 Documentary 25
## 11 Mystery 16
## 12 Sci-Fi 7
## 13 Family 3
## 14 Musical 2
## 15 Romance 2
## 16 Western 2
## 17 Thriller 1- Produce a table with the average gross earning and budget (
grossandbudget) by genre. Calculate a variablereturn_on_budgetwhich shows how many $ did a movie make at the box office for each $ of its budget. Ranked genres by thisreturn_on_budgetin descending order
movies %>%
group_by(genre) %>%
summarise(
avg_gross_earn = mean(gross),
avg_gross_budget = mean(budget)) %>%
mutate(return_on_budget = avg_gross_earn/avg_gross_budget) %>% #calculate $ made per $ spent
arrange(desc(return_on_budget))## # A tibble: 17 × 4
## genre avg_gross_earn avg_gross_budget return_on_budget
## <chr> <dbl> <dbl> <dbl>
## 1 Musical 92084000 3189500 28.9
## 2 Family 149160478. 14833333. 10.1
## 3 Western 20821884 3465000 6.01
## 4 Documentary 17353973. 5887852. 2.95
## 5 Horror 37713738. 13504916. 2.79
## 6 Fantasy 42408841. 17582143. 2.41
## 7 Comedy 42630552. 24446319. 1.74
## 8 Mystery 67533021. 39218750 1.72
## 9 Animation 98433792. 61701429. 1.60
## 10 Biography 45201805. 28543696. 1.58
## 11 Adventure 95794257. 66290069. 1.45
## 12 Drama 37465371. 26242933. 1.43
## 13 Crime 37502397. 26596169. 1.41
## 14 Romance 31264848. 25107500 1.25
## 15 Action 86583860. 71354888. 1.21
## 16 Sci-Fi 29788371. 27607143. 1.08
## 17 Thriller 2468 300000 0.00823- Produce a table that shows the top 15 directors who have created the highest gross revenue in the box office. Don’t just show the total gross amount, but also the mean, median, and standard deviation per director.
movies %>%
group_by(director) %>%
summarise(
gross_rev = sum(gross),
mean_gross_rev = mean(gross),
median_gross_rev = median(gross),
std_gross_rev = StdDev(gross)) %>%
slice_max(order_by = gross_rev, n=15) #deriving top 15 directors by gross revenue## # A tibble: 15 × 5
## director gross_rev mean_gross_rev median_gross_rev std_gross_rev[…¹
## <chr> <dbl> <dbl> <dbl> <dbl>
## 1 Steven Spielberg 4014061704 174524422. 164435221 101421051.
## 2 Michael Bay 2231242537 171634041. 138396624 127161579.
## 3 Tim Burton 2071275480 129454718. 76519172 108726924.
## 4 Sam Raimi 2014600898 201460090. 234903076 162126632.
## 5 James Cameron 1909725910 318287652. 175562880. 309171337.
## 6 Christopher Nolan 1813227576 226653447 196667606. 187224133.
## 7 George Lucas 1741418480 348283696 380262555 146193880.
## 8 Robert Zemeckis 1619309108 124562239. 100853835 91300279.
## 9 Clint Eastwood 1378321100 72543216. 46700000 75487408.
## 10 Francis Lawrence 1358501971 271700394. 281666058 135437020.
## 11 Ron Howard 1335988092 111332341 101587923 81933761.
## 12 Gore Verbinski 1329600995 189942999. 123207194 154473822.
## 13 Andrew Adamson 1137446920 284361730 279680930. 120895765.
## 14 Shawn Levy 1129750988 102704635. 85463309 65484773.
## 15 Ridley Scott 1128857598 80632686. 47775715 68812285.
## # … with abbreviated variable name ¹std_gross_rev[,1]- Finally, ratings. Produce a table that describes how ratings are distributed by genre. We don’t want just the mean, but also, min, max, median, SD and some kind of a histogram or density graph that visually shows how ratings are distributed.
top <- movies %>%
group_by(genre) %>%
summarise(
mean_rating = mean(rating),
min_rating = min(rating),
max_rating=max(rating),
median_rating=median(rating),
std_rating = StdDev(rating))
top #print the table## # A tibble: 17 × 6
## genre mean_rating min_rating max_rating median_rating std_rating[,1]
## <chr> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 Action 6.23 2.1 9 6.3 1.03
## 2 Adventure 6.51 2.3 8.6 6.6 1.09
## 3 Animation 6.65 4.5 8 6.9 0.968
## 4 Biography 7.11 4.5 8.9 7.2 0.760
## 5 Comedy 6.11 1.9 8.8 6.2 1.02
## 6 Crime 6.92 4.8 9.3 6.9 0.849
## 7 Documentary 6.66 1.6 8.5 7.4 1.77
## 8 Drama 6.73 2.1 8.8 6.8 0.917
## 9 Family 6.5 5.7 7.9 5.9 1.22
## 10 Fantasy 6.15 4.3 7.9 6.45 0.959
## 11 Horror 5.83 3.6 8.5 5.9 1.01
## 12 Musical 6.75 6.3 7.2 6.75 0.636
## 13 Mystery 6.86 4.6 8.5 6.9 0.882
## 14 Romance 6.65 6.2 7.1 6.65 0.636
## 15 Sci-Fi 6.66 5 8.2 6.4 1.09
## 16 Thriller 4.8 4.8 4.8 4.8 NA
## 17 Western 5.7 4.1 7.3 5.7 2.26ggplot(top, mapping=aes(x=mean_rating)) +
geom_histogram(binwidth=0.5) + #creating histogram distributing mean movie rating
labs(
title = "Ratings Distributed by Genre",
x = "Means Ratings",
y = "Count"
) +
theme_bw(base_size = 9)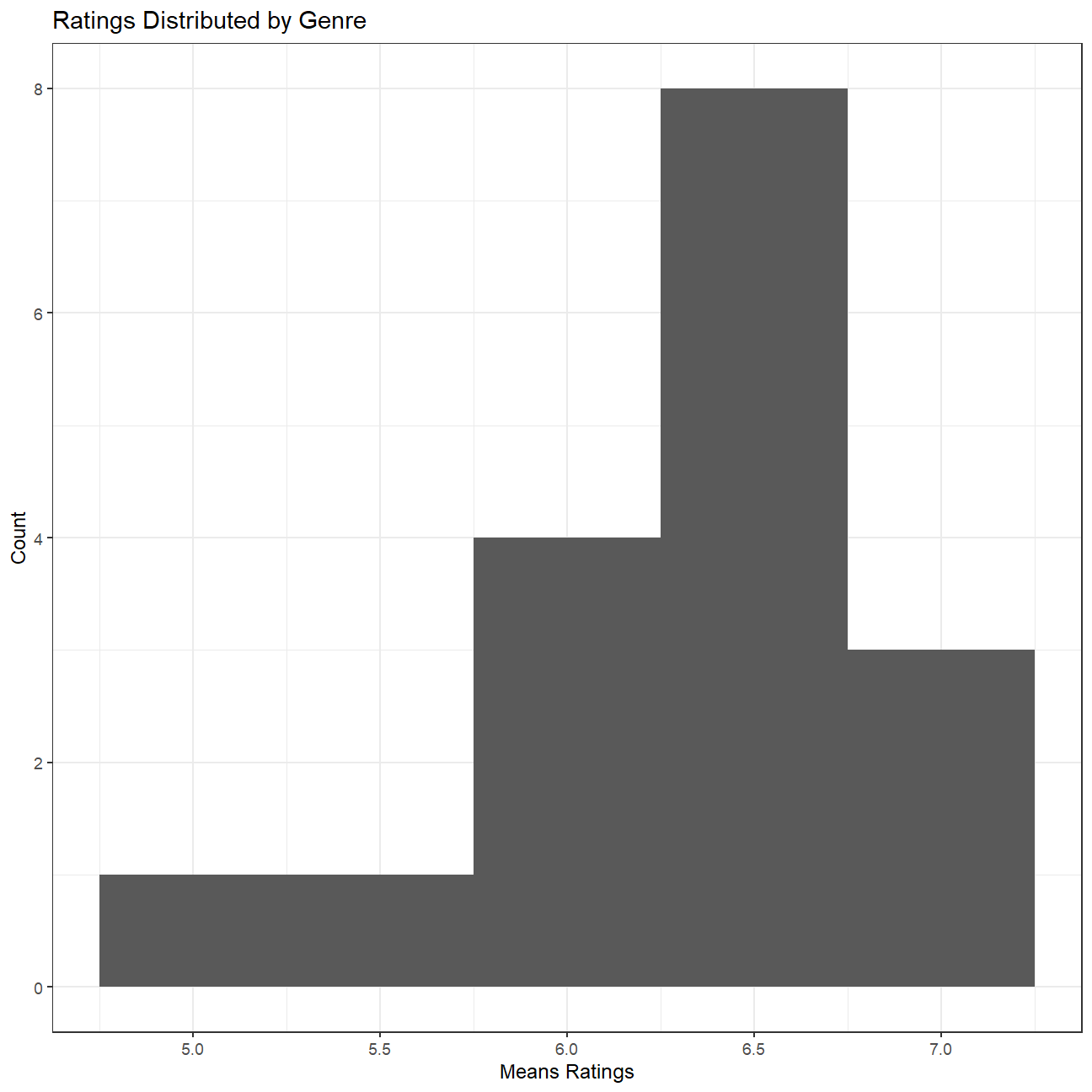
Use ggplot to answer the following
- Examine the relationship between
grossandcast_facebook_likes. Produce a scatterplot and write one sentence discussing whether the number of facebook likes that the cast has received is likely to be a good predictor of how much money a movie will make at the box office. What variable are you going to map to the Y- and X- axes?
There is a common assumption that the number of facebook likes depicts the popularity of the cast and hence, would also lead to more movie-goers but this scatter plot shows that there are some significant outliers and thus, there is a very slight positive correlation.
We have mapped gross to x-axis and cast_facebook_likes on the y-axis.
movies %>%
ggplot(mapping=aes(x=gross, y=cast_facebook_likes)) +
geom_point() +
geom_smooth(method = "lm", se = FALSE) + #create line of best fit
labs(
title = "Scatterplot for Facebook Likes v Gross Earnings at Box Office",
x = "Gross Earnings",
y = "Facebook Likes received Cast"
) +
theme_bw(base_size = 14)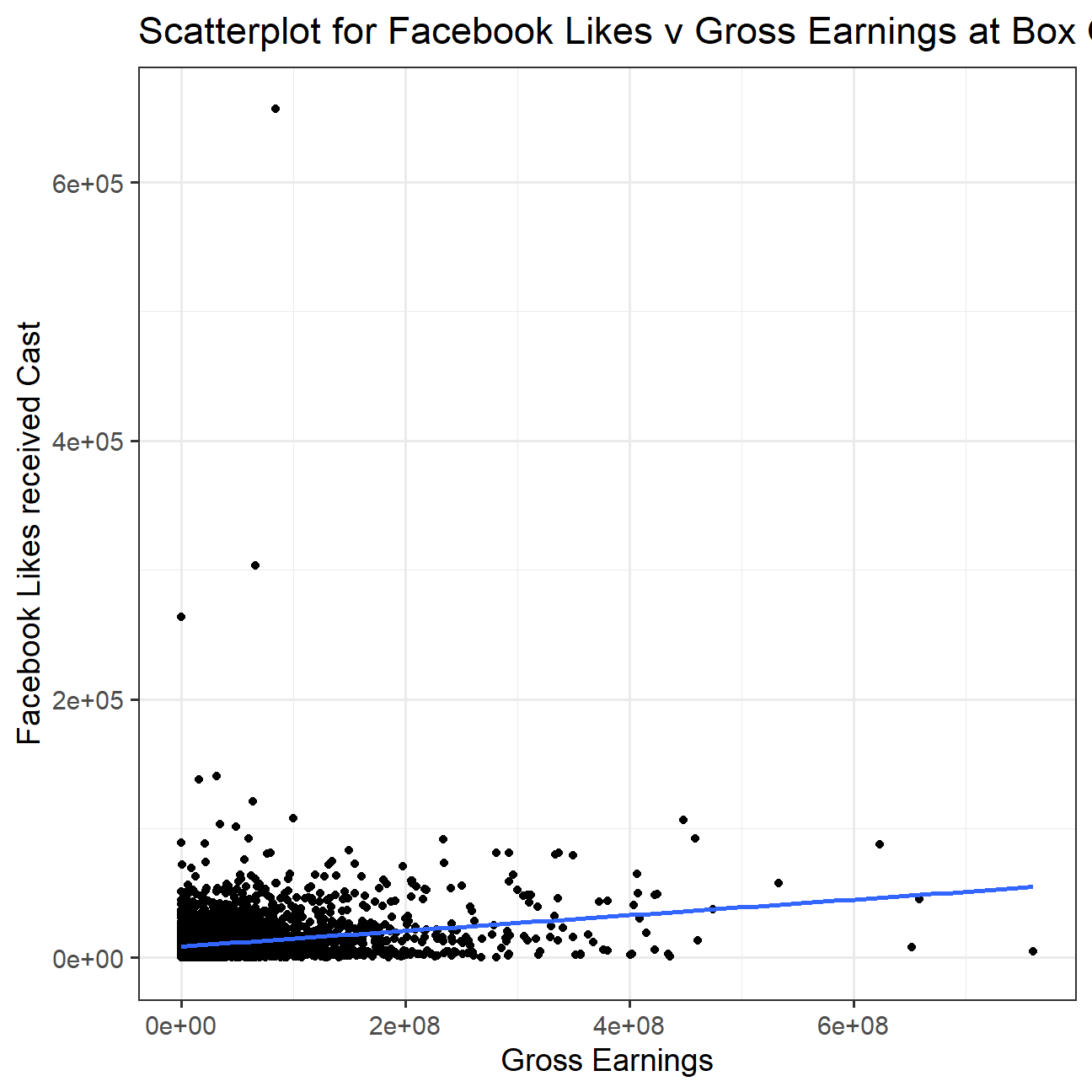
- Examine the relationship between
grossandbudget. Produce a scatterplot and write one sentence discussing whether budget is likely to be a good predictor of how much money a movie will make at the box office.
The scatter plot shows that there is a positive correlation between budgets and gross earnings, which can be because big budgets means big money for special effects, marketing and larger distribution world-wide, which attracts more audience.
movies %>%
ggplot(mapping=aes(x=budget, y=gross)) +
geom_smooth(method = "lm", se = FALSE) + #create line of best fit
labs(
title = "Scatterplot for Gross vs Budget",
x = "Budget",
y = "Gross"
) +
geom_point() +
theme_bw(base_size = 14)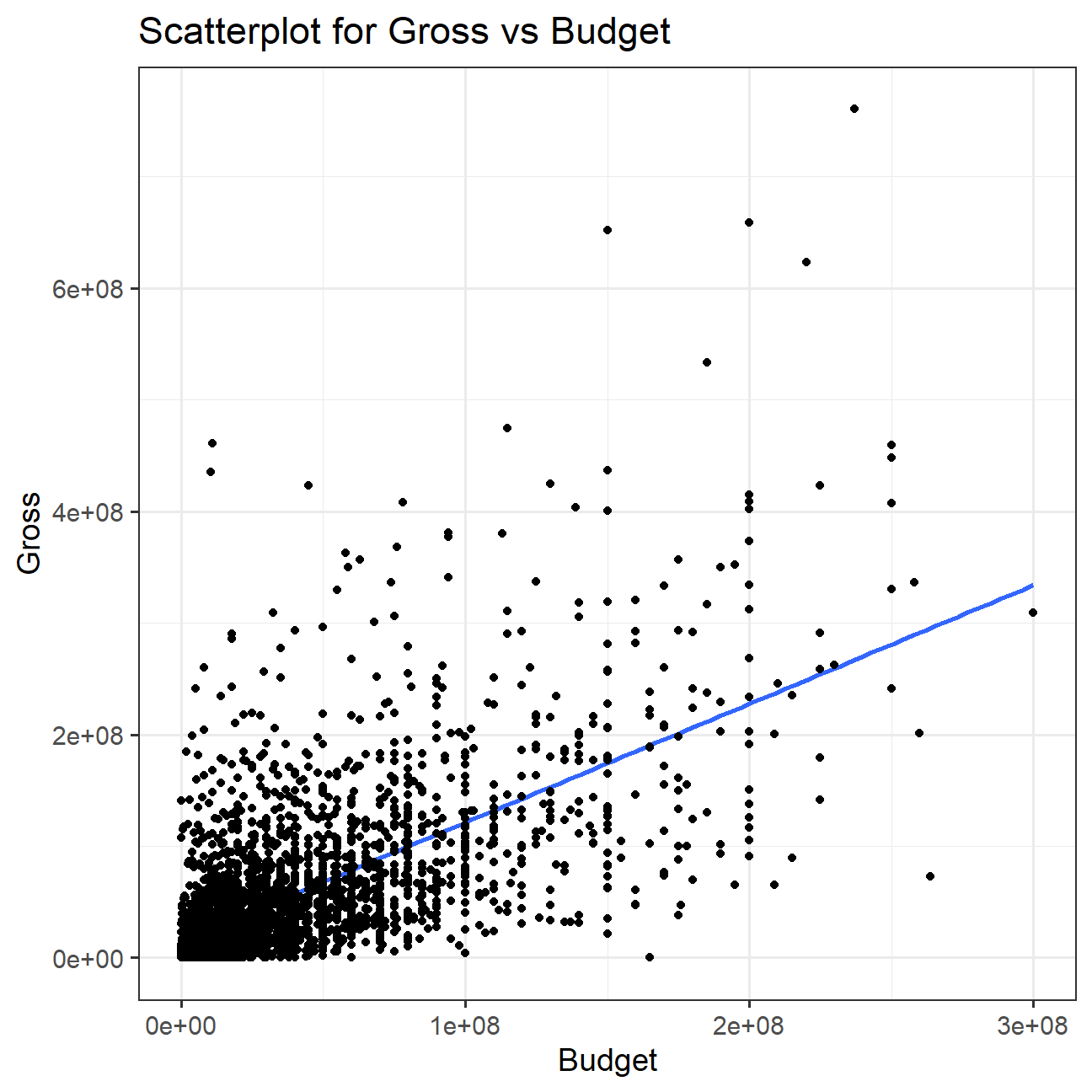
- Examine the relationship between
grossandrating. Produce a scatterplot, faceted bygenreand discuss whether IMDB ratings are likely to be a good predictor of how much money a movie will make at the box office. Is there anything strange in this dataset?
For some of the genres, like action and adventure, high IMDB ratings correlate to higher gross earnings. This could be because action and adventure movies have a higher mass appeal. However, for some genres like thriller and western, we don’t have enough data make an educated statement of the relationship between the two variables.
The strange thing is that documentary and sci-fi have a declining line of best fit, which shows a slight negative correlation.
movies %>%
ggplot(mapping=aes(x=rating, y=gross)) +
geom_point() +
geom_smooth(method = "lm", se = FALSE) + #create line of best fit
labs(
title = "Scatterplot for Gross vs Ratings per Genre",
x = "Ratings",
y = "Gross"
) +
facet_wrap(~genre) +
theme_bw(base_size = 14)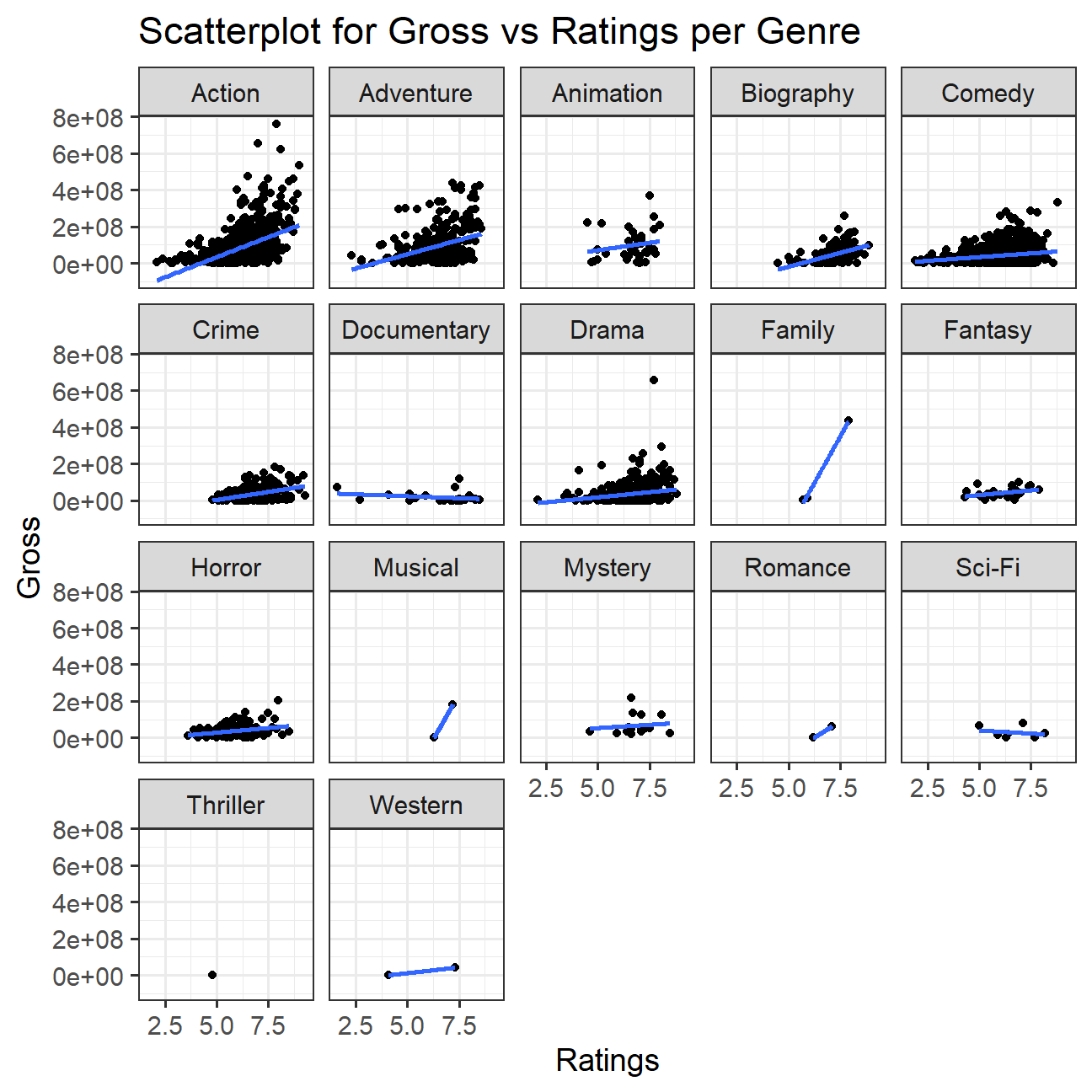
Returns of financial stocks
We must first identify which stocks we want to download data for, and for this we must know their ticker symbol; Apple is known as AAPL, Microsoft as MSFT, McDonald’s as MCD, etc. The file nyse.csv contains 508 stocks listed on the NYSE, their ticker symbol, name, the IPO (Initial Public Offering) year, and the sector and industry the company is in.
nyse <- read_csv(here::here("data","nyse.csv"))Based on this dataset, create a table and a bar plot that shows the number of companies per sector, in descending order
nyse1 <- nyse %>%
group_by(sector) %>%
summarise(count_comp=count(sector))%>%
mutate(
sector=fct_reorder(sector,count_comp,.desc=TRUE)) %>% #arrange sectors by no. of companies
arrange(desc(count_comp))
ggplot(nyse1, aes(x=sector,y=count_comp)) +
geom_col() +
labs(
title = "Frequency of Companies per Sector",
x = "Sector",
y = "Frequency of Companies"
) +
theme_bw(base_size=14) +
theme(axis.text.x = element_text(angle = 90, hjust = 1))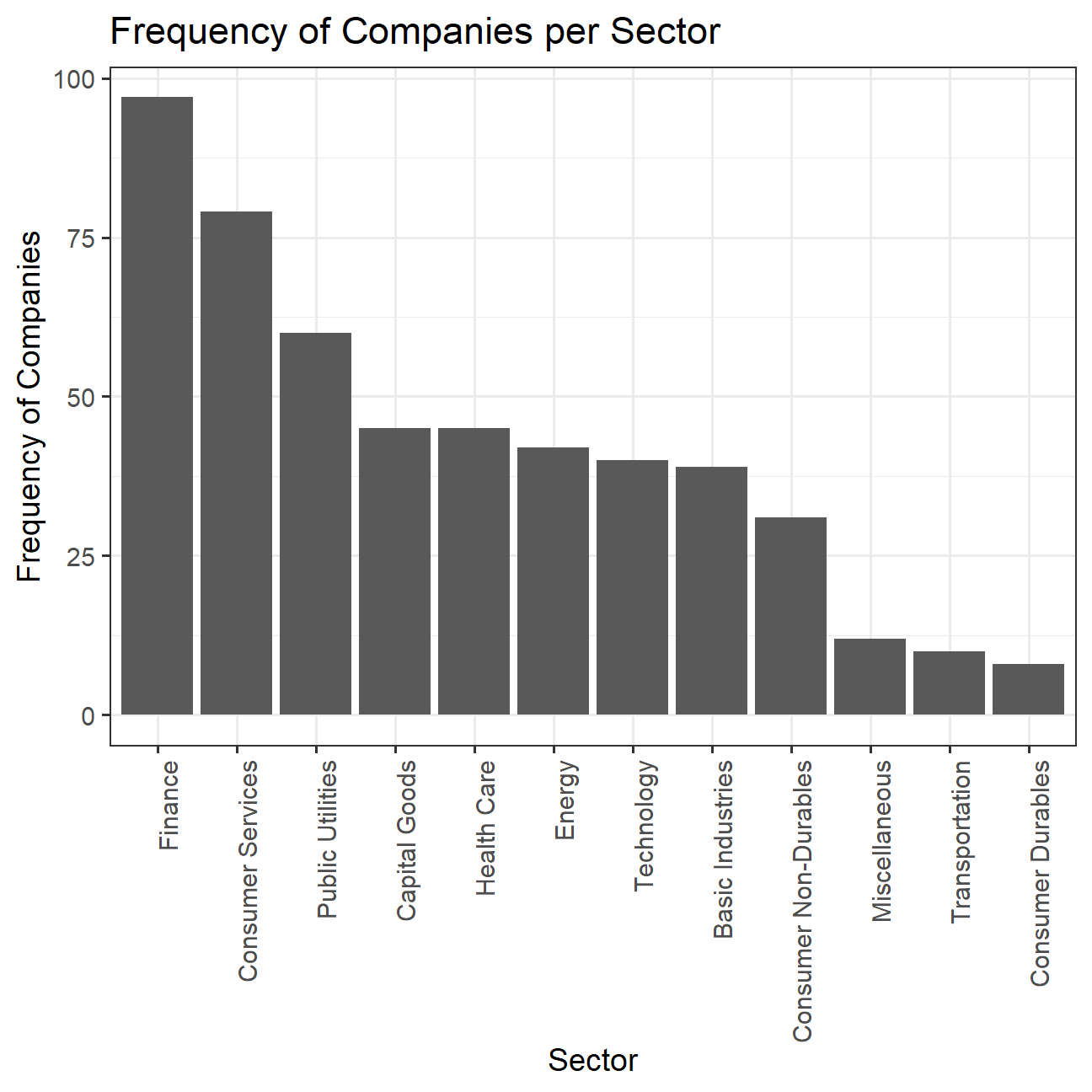
nyse1 #print the table## # A tibble: 12 × 2
## sector count_comp
## <fct> <int>
## 1 Finance 97
## 2 Consumer Services 79
## 3 Public Utilities 60
## 4 Capital Goods 45
## 5 Health Care 45
## 6 Energy 42
## 7 Technology 40
## 8 Basic Industries 39
## 9 Consumer Non-Durables 31
## 10 Miscellaneous 12
## 11 Transportation 10
## 12 Consumer Durables 8Next, let’s choose some stocks and their ticker symbols and download some data.
myStocks <- c("SPY","A","Y","CMG","EVRG","IT","PKX" ) %>%
tq_get(get = "stock.prices",
from = "2011-01-01",
to = "2022-08-31") %>%
group_by(symbol)
glimpse(myStocks) # examine the structure of the resulting data frame## Rows: 20,545
## Columns: 8
## Groups: symbol [7]
## $ symbol <chr> "SPY", "SPY", "SPY", "SPY", "SPY", "SPY", "SPY", "SPY", "SPY"…
## $ date <date> 2011-01-03, 2011-01-04, 2011-01-05, 2011-01-06, 2011-01-07, …
## $ open <dbl> 127, 127, 127, 128, 128, 127, 127, 128, 129, 128, 129, 129, 1…
## $ high <dbl> 128, 127, 128, 128, 128, 127, 128, 129, 129, 129, 130, 130, 1…
## $ low <dbl> 126, 126, 126, 127, 126, 126, 127, 127, 128, 128, 129, 128, 1…
## $ close <dbl> 127, 127, 128, 127, 127, 127, 127, 129, 128, 129, 130, 128, 1…
## $ volume <dbl> 1.39e+08, 1.37e+08, 1.34e+08, 1.23e+08, 1.56e+08, 1.22e+08, 1…
## $ adjusted <dbl> 102, 102, 102, 102, 102, 102, 102, 103, 103, 104, 104, 103, 1…Financial performance analysis depend on returns; If I buy a stock today for 100 and I sell it tomorrow for 101.75, my one-day return, assuming no transaction costs, is 1.75%. So given the adjusted closing prices, our first step is to calculate daily and monthly returns.
#calculate daily returns
myStocks_returns_daily <- myStocks %>%
tq_transmute(select = adjusted,
mutate_fun = periodReturn,
period = "daily",
type = "log",
col_rename = "daily_returns",
cols = c(nested.col))
#calculate monthly returns
myStocks_returns_monthly <- myStocks %>%
tq_transmute(select = adjusted,
mutate_fun = periodReturn,
period = "monthly",
type = "arithmetic",
col_rename = "monthly_returns",
cols = c(nested.col))
#calculate yearly returns
myStocks_returns_annual <- myStocks %>%
group_by(symbol) %>%
tq_transmute(select = adjusted,
mutate_fun = periodReturn,
period = "yearly",
type = "arithmetic",
col_rename = "yearly_returns",
cols = c(nested.col))Create a table where you summarise monthly returns for each of the stocks and SPY; min, max, median, mean, SD.
myStocks_returns_monthly %>%
group_by(symbol) %>%
summarise(
median_return = median(monthly_returns),
min_return = min(monthly_returns),
max_return = max(monthly_returns),
mean_return = mean(monthly_returns),
sd_return = sd(monthly_returns))## # A tibble: 7 × 6
## symbol median_return min_return max_return mean_return sd_return
## <chr> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 A 0.0125 -0.175 0.216 0.0135 0.0697
## 2 CMG 0.0155 -0.231 0.343 0.0186 0.0949
## 3 EVRG 0.0130 -0.171 0.152 0.0117 0.0518
## 4 IT 0.0281 -0.230 0.266 0.0184 0.0763
## 5 PKX -0.00484 -0.226 0.200 -0.00222 0.0845
## 6 SPY 0.0146 -0.125 0.127 0.0106 0.0404
## 7 Y 0.00623 -0.160 0.280 0.00901 0.0543Plot a density plot, using geom_density(), for each of the stocks
ggplot(data = myStocks_returns_monthly,aes(monthly_returns)) +
geom_density() +
facet_wrap(~symbol) +
labs(
title = "Density Plot for the Choosen Stocks",
x = NULL,
y = NULL
) +
theme_bw(base_size = 14)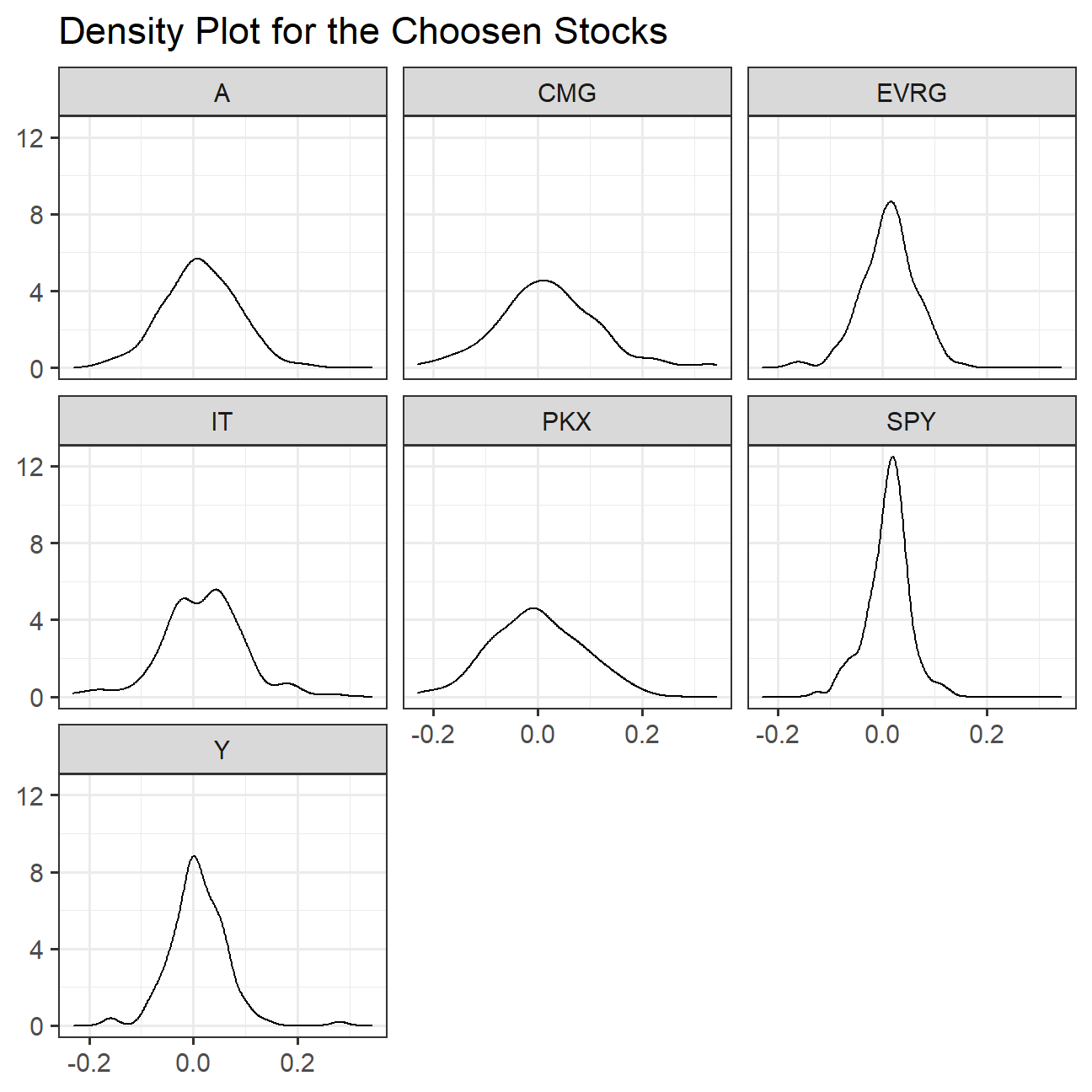
What can you infer from this plot? Which stock is the riskiest? The least risky?
If we consider the performance of SPY to be the performance of the broader market, then we can learn that the stocks A, CMG, PKX, and Y have lagged the broader market in terms of return performance in more months. However, returns are only part of the picture and we must not forget the risks. In this chart, the dispersion of the data reflects the risk profile of the stock, the more even the density, the higher the risk, as this means that it is difficult for us to predict the performance of this stock. Therefore, A, CMG and PKG are thus probably the riskiest, and SPY is the least risky.
Finally, make a plot that shows the expected monthly return (mean) of a stock on the Y axis and the risk (standard deviation) in the X-axis. Please use ggrepel::geom_text_repel() to label each stock
myStocks_returns_monthly %>%
group_by(symbol) %>%
summarise(
sd_return = sd(monthly_returns),
mean_return = mean(monthly_returns)
) %>%
ggplot(aes(mean_return, sd_return, label=symbol)) +
geom_point() +
ggrepel::geom_text_repel() + #add labels to the scatterplot points
labs(
title = "Risk vs Return Scatter Plot",
x = "Mean of Expected Monthly Return",
y = "Risk"
) +
theme_bw(base_size = 14)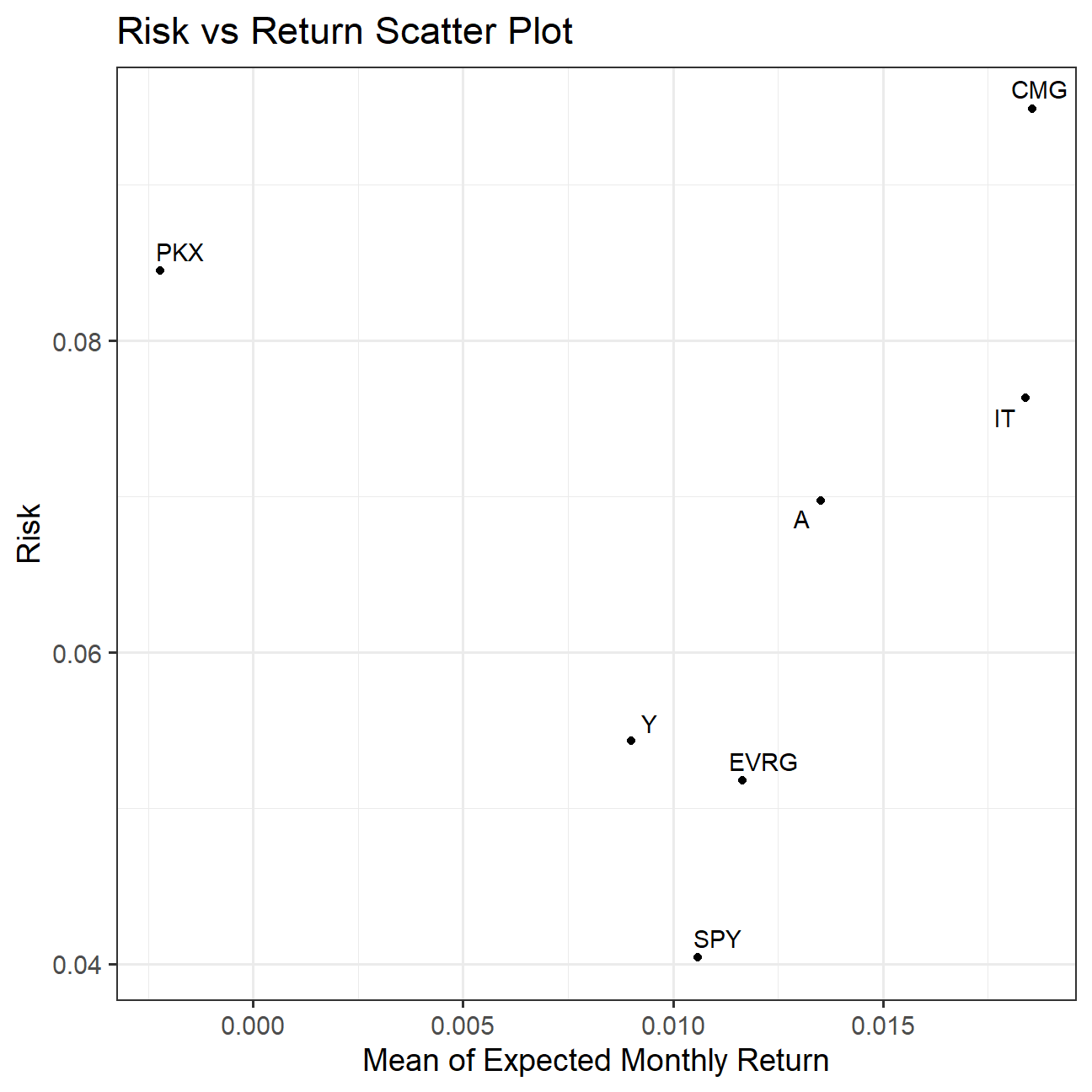
What can you infer from this plot? Are there any stocks which, while being riskier, do not have a higher expected return?
The x-axis of this graph represents average monthly returns and the y-axis represents risk. We can see that most of the points follow the common perception that higher the risk, higher the reward. But of all the 7 stocks, SPY has the lowest risk for a proportionally higher return and there does exist one stock, PKX which is riskier but does not have a high expected return.
On your own: Spotify
spotify_songs <- readr::read_csv('https://raw.githubusercontent.com/rfordatascience/tidytuesday/master/data/2020/2020-01-21/spotify_songs.csv')The data dictionary can be found below
| variable | class | description |
|---|---|---|
| track_id | character | Song unique ID |
| track_name | character | Song Name |
| track_artist | character | Song Artist |
| track_popularity | double | Song Popularity (0-100) where higher is better |
| track_album_id | character | Album unique ID |
| track_album_name | character | Song album name |
| track_album_release_date | character | Date when album released |
| playlist_name | character | Name of playlist |
| playlist_id | character | Playlist ID |
| playlist_genre | character | Playlist genre |
| playlist_subgenre | character | Playlist subgenre |
| danceability | double | Danceability describes how suitable a track is for dancing based on a combination of musical elements including tempo, rhythm stability, beat strength, and overall regularity. A value of 0.0 is least danceable and 1.0 is most danceable. |
| energy | double | Energy is a measure from 0.0 to 1.0 and represents a perceptual measure of intensity and activity. Typically, energetic tracks feel fast, loud, and noisy. For example, death metal has high energy, while a Bach prelude scores low on the scale. Perceptual features contributing to this attribute include dynamic range, perceived loudness, timbre, onset rate, and general entropy. |
| key | double | The estimated overall key of the track. Integers map to pitches using standard Pitch Class notation . E.g. 0 = C, 1 = C♯/D♭, 2 = D, and so on. If no key was detected, the value is -1. |
| loudness | double | The overall loudness of a track in decibels (dB). Loudness values are averaged across the entire track and are useful for comparing relative loudness of tracks. Loudness is the quality of a sound that is the primary psychological correlate of physical strength (amplitude). Values typical range between -60 and 0 db. |
| mode | double | Mode indicates the modality (major or minor) of a track, the type of scale from which its melodic content is derived. Major is represented by 1 and minor is 0. |
| speechiness | double | Speechiness detects the presence of spoken words in a track. The more exclusively speech-like the recording (e.g. talk show, audio book, poetry), the closer to 1.0 the attribute value. Values above 0.66 describe tracks that are probably made entirely of spoken words. Values between 0.33 and 0.66 describe tracks that may contain both music and speech, either in sections or layered, including such cases as rap music. Values below 0.33 most likely represent music and other non-speech-like tracks. |
| acousticness | double | A confidence measure from 0.0 to 1.0 of whether the track is acoustic. 1.0 represents high confidence the track is acoustic. |
| instrumentalness | double | Predicts whether a track contains no vocals. “Ooh” and “aah” sounds are treated as instrumental in this context. Rap or spoken word tracks are clearly “vocal”. The closer the instrumentalness value is to 1.0, the greater likelihood the track contains no vocal content. Values above 0.5 are intended to represent instrumental tracks, but confidence is higher as the value approaches 1.0. |
| liveness | double | Detects the presence of an audience in the recording. Higher liveness values represent an increased probability that the track was performed live. A value above 0.8 provides strong likelihood that the track is live. |
| valence | double | A measure from 0.0 to 1.0 describing the musical positiveness conveyed by a track. Tracks with high valence sound more positive (e.g. happy, cheerful, euphoric), while tracks with low valence sound more negative (e.g. sad, depressed, angry). |
| tempo | double | The overall estimated tempo of a track in beats per minute (BPM). In musical terminology, tempo is the speed or pace of a given piece and derives directly from the average beat duration. |
| duration_ms | double | Duration of song in milliseconds |
In this dataset, there are only 6 types of playlist_genre , but we can still try to perform EDA on this dataset.
Produce a one-page summary describing this dataset. Here is a non-exhaustive list of questions:
- What is the distribution of songs’ popularity (
track_popularity). Does it look like a Normal distribution?
No, the track popularity does not look like a normal distribution.
popularity <- spotify_songs['track_popularity'] #extract track popularity from the dataset
ggplot(popularity, aes(x=track_popularity))+
geom_histogram()+
labs(
title= "Distribution of Popularity",
x="Popularity",
y=NULL) +
theme_bw(base_size = 14)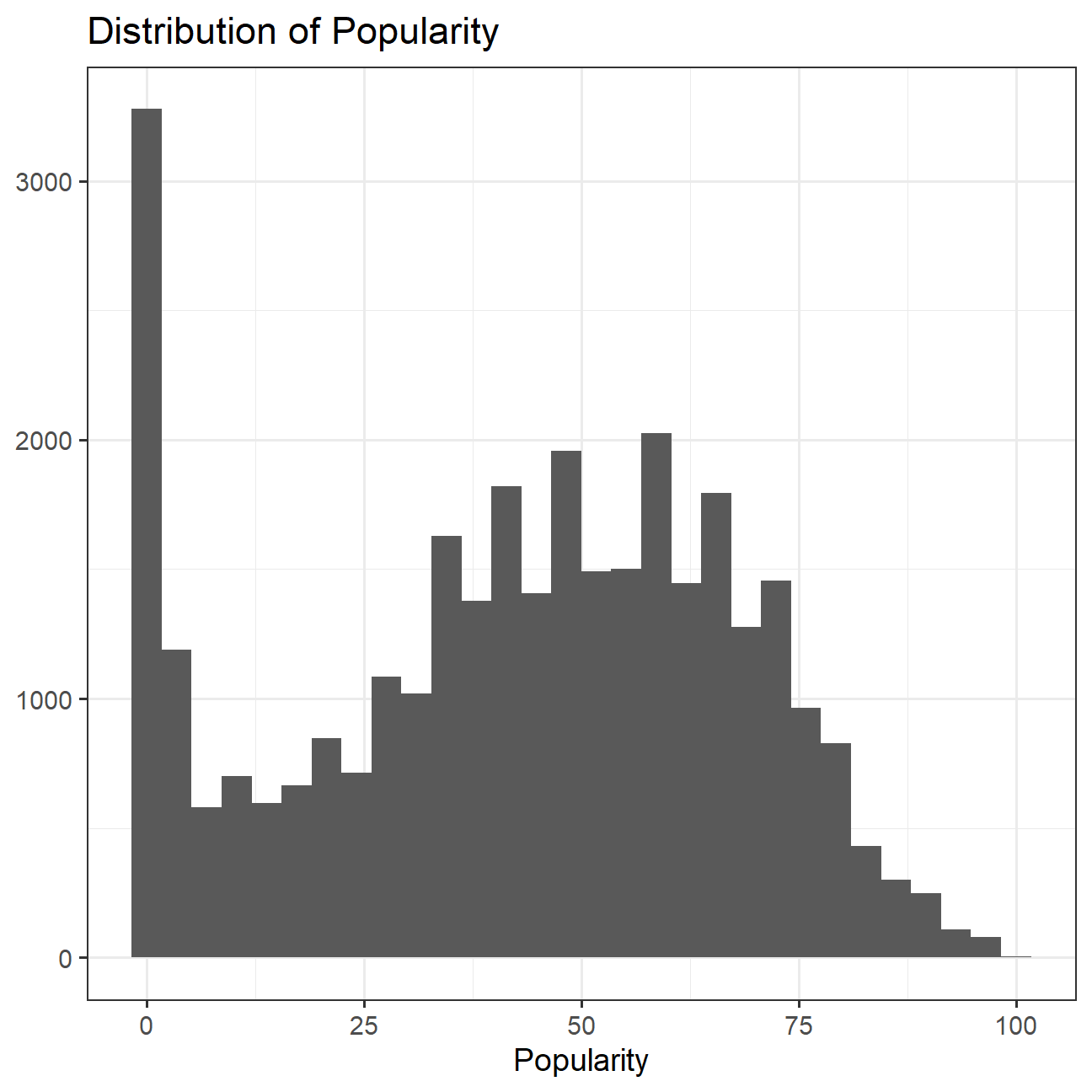
- There are 12 audio features for each track, including confidence measures like
acousticness,liveness,speechinesandinstrumentalness, perceptual measures likeenergy,loudness,danceabilityandvalence(positiveness), and descriptors likeduration,tempo,key, andmode. How are they distributed? can you roughly guess which of these variables is closer to Normal just by looking at summary statistics?
As shown below in the summary statistics of the 12 audio features. We could guess roughly that ‘tempo’, danceability, energy, instrumentalness are closer to the normal distribution because their mean and median are roughly equal, and they have similar value for 1st quartile and 3rd quartile.
features <- c('speechiness', 'acousticness', 'liveness', 'instrumentalness', 'duration_ms', 'energy', 'loudness', 'danceability', 'valence', 'tempo', 'key', 'mode')
summary_spotify <- summary(spotify_songs[features])
summary_spotify## speechiness acousticness liveness instrumentalness
## Min. :0.000 Min. :0.000 Min. :0.000 Min. :0.000
## 1st Qu.:0.041 1st Qu.:0.015 1st Qu.:0.093 1st Qu.:0.000
## Median :0.062 Median :0.080 Median :0.127 Median :0.000
## Mean :0.107 Mean :0.175 Mean :0.190 Mean :0.085
## 3rd Qu.:0.132 3rd Qu.:0.255 3rd Qu.:0.248 3rd Qu.:0.005
## Max. :0.918 Max. :0.994 Max. :0.996 Max. :0.994
## duration_ms energy loudness danceability
## Min. : 4000 Min. :0.000 Min. :-46.4 Min. :0.000
## 1st Qu.:187819 1st Qu.:0.581 1st Qu.: -8.2 1st Qu.:0.563
## Median :216000 Median :0.721 Median : -6.2 Median :0.672
## Mean :225800 Mean :0.699 Mean : -6.7 Mean :0.655
## 3rd Qu.:253585 3rd Qu.:0.840 3rd Qu.: -4.6 3rd Qu.:0.761
## Max. :517810 Max. :1.000 Max. : 1.3 Max. :0.983
## valence tempo key mode
## Min. :0.000 Min. : 0 Min. : 0.00 Min. :0.000
## 1st Qu.:0.331 1st Qu.:100 1st Qu.: 2.00 1st Qu.:0.000
## Median :0.512 Median :122 Median : 6.00 Median :1.000
## Mean :0.511 Mean :121 Mean : 5.37 Mean :0.566
## 3rd Qu.:0.693 3rd Qu.:134 3rd Qu.: 9.00 3rd Qu.:1.000
## Max. :0.991 Max. :239 Max. :11.00 Max. :1.000- Is there any relationship between
valenceandtrack_popularity?danceabilityandtrack_popularity?
The correlation between valence and track_popularity is 0.032, and danceability and track_popularity is 0.0647, so they are not obviously related to each other.
ggplot(spotify_songs,aes(x=valence,y=track_popularity)) +
geom_point() +
labs(
title="Valence and Popularity",
x="Valence",
y="Track popularity") +
theme_bw(base_size = 14)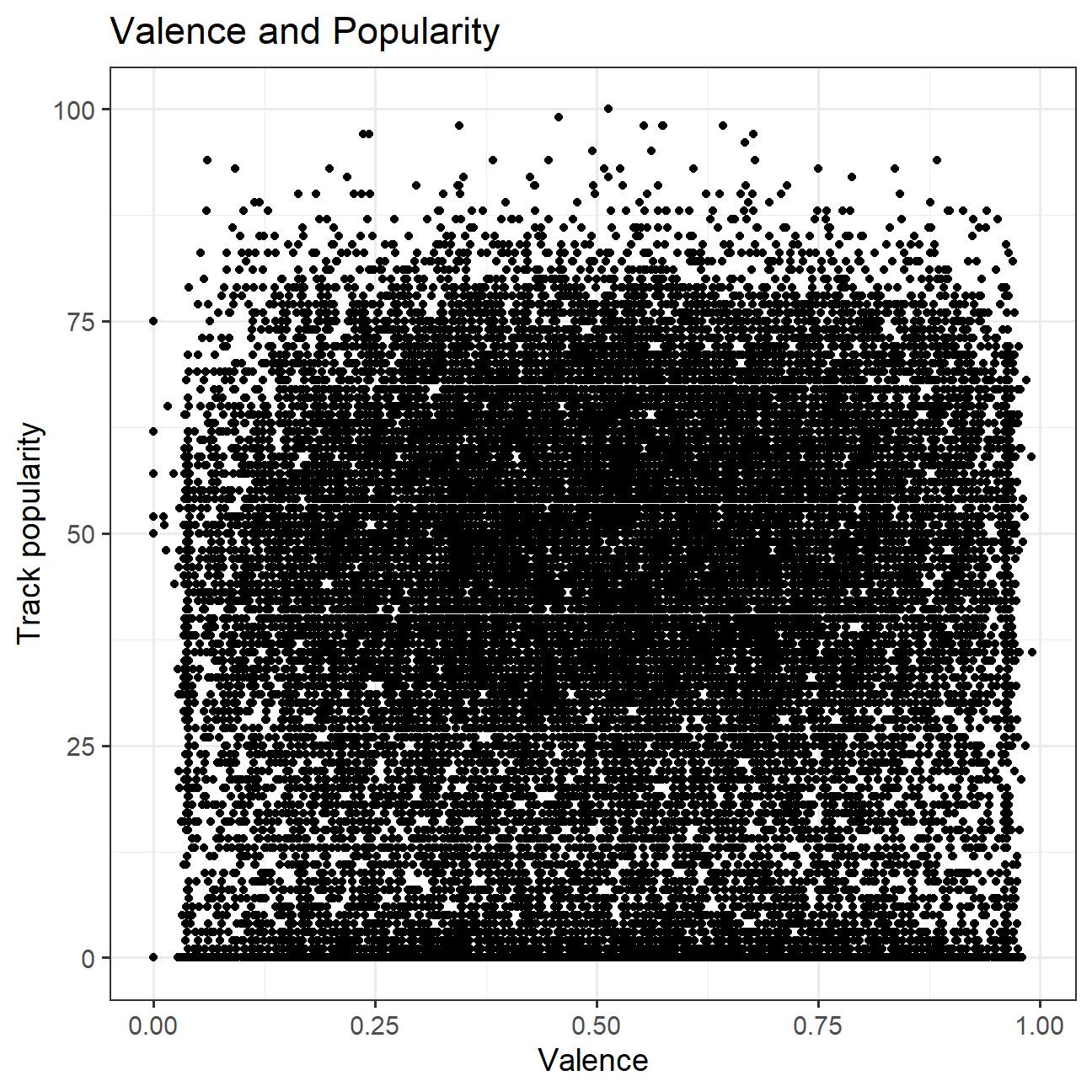
cor_vp <- cor(spotify_songs$valence,spotify_songs$track_popularity) #find coeff of correlation
cor_vp## [1] 0.0332ggplot(spotify_songs,aes(x=danceability,y=track_popularity)) +
geom_point() +
labs(
title="Danceability and Popularity",
x="Danceability",
y="Track popularity") +
theme_bw(base_size = 14)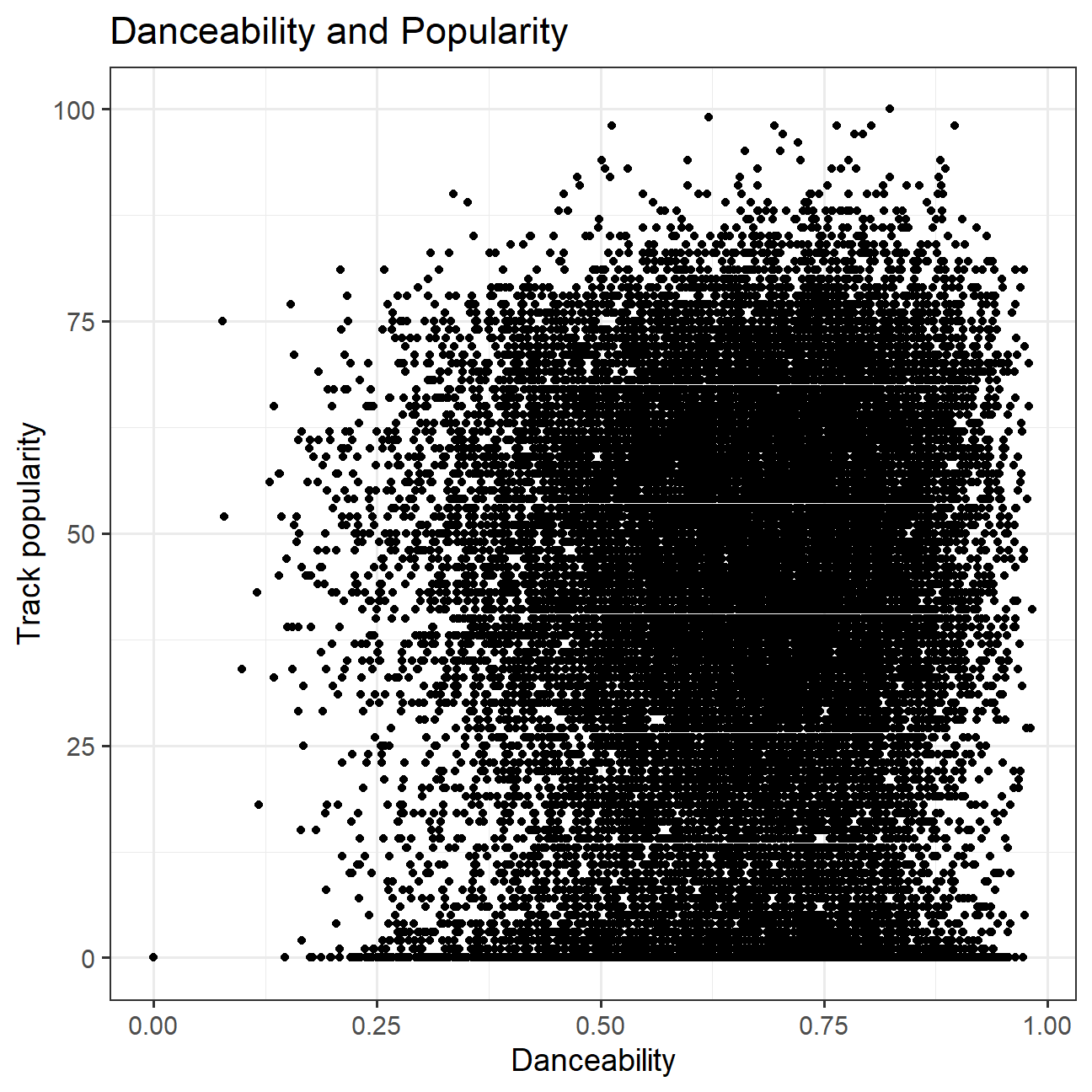
cor_dt <- cor(spotify_songs$danceability,spotify_songs$track_popularity) #find coeff of correlation
cor_dt## [1] 0.0647modeindicates the modality (major or minor) of a track, the type of scale from which its melodic content is derived. Major is represented by 1 and minor is 0. Do songs written on a major scale have higherdanceabilitycompared to those in minor scale? What abouttrack_popularity?
We can find that major songs, according to this dataset, no matter the mean or median, have more popularity, whereas minor songs have larger danceability, but the difference is little.
major <- spotify_songs %>%
filter(mode == 1) #filter for major song
major %>%
summarise(major_mean_d=mean(major$danceability),
major_mean_p=mean(major$track_popularity),
major_median_d=median(major$danceability),
major_median_p=median(major$track_popularity))## # A tibble: 1 × 4
## major_mean_d major_mean_p major_median_d major_median_p
## <dbl> <dbl> <dbl> <dbl>
## 1 0.647 42.7 0.663 46minor <- spotify_songs %>%
filter(mode == 0) #filter for minor song
minor %>%
summarise(minor_mean_d=mean(minor$danceability),
minor_mean_p=mean(minor$track_popularity),
minor_median_d=median(minor$danceability),
minor_median_p=median(minor$track_popularity))## # A tibble: 1 × 4
## minor_mean_d minor_mean_p minor_median_d minor_median_p
## <dbl> <dbl> <dbl> <dbl>
## 1 0.665 42.2 0.68 45Challenge 1: Replicating a chart
Create a graph that calculates the cumulative % change for 0-, 1-, and 2-bed flats between 2000 and 2018 for the top twelve cities in Bay Area, by number of ads that appeared in Craigslist.
library(scales)
top_12_cities <- rent %>%
group_by(city) %>%
summarise(count_city = count(city)) %>%
arrange(desc(count_city)) %>%
slice_head(n = 12) #derive top 12 after arranging in descending order by no. of city
rent_12_cities <- rent %>%
filter(city %in% c(top_12_cities$city))
medianPricePerCity <- rent_12_cities %>%
group_by(city,beds,year) %>% #aggregating per city, bed and year
summarise(mean_price = median(price)) %>%
filter(beds < 3) %>%
arrange(city,beds,year)
cum_top_12 <- medianPricePerCity %>%
group_by(city,beds) %>%
mutate(pct_change = (mean_price/lag(mean_price))) %>% #calculate change in price from prev row
mutate(pct_change = ifelse(is.na(pct_change), 1, pct_change)) %>% #replace blank values with 100%
mutate(cumulative_change = cumprod(pct_change)) #calculate cumm % change
ggplot(cum_top_12,aes(x = year, y = cumulative_change,color= city)) +
geom_line() +
facet_grid(beds ~ city,scales= "free_y") + #scale of y is not fixed
theme_bw(base_size = 14) +
theme(
legend.position = "none",
axis.text.x = element_text(angle = 90)) +
scale_y_continuous(labels = scales::percent_format(scale = 100)) + #y-axis in % format
scale_x_continuous(breaks = seq(2005, 2018, by = 5)) +
labs(title = "Cumulative % change in 0,1, and 2-bed rentals in Bay Area",
subtitle = "2000-2018")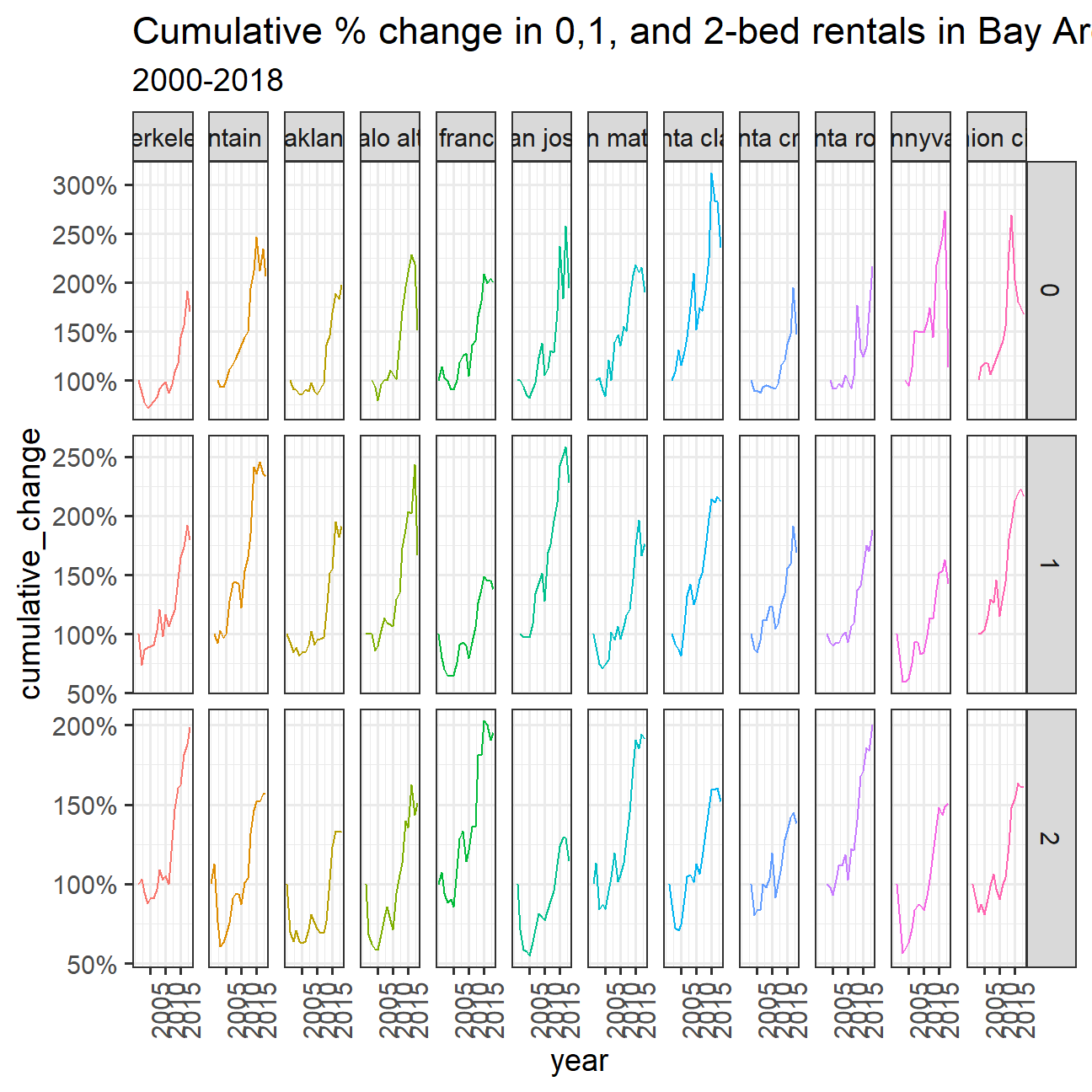
Challenge 2: 2016 California Contributors plots
Reproduce the plot that shows the top ten cities in highest amounts raised in political contributions in California during the 2016 US Presidential election.
library(patchwork)
CA_contributors_2016 <- vroom::vroom(here::here("data","CA_contributors_2016.csv")) #reading the csv file
CA_contributors <- CA_contributors_2016 %>%
mutate(zip=as.character(zip)) #changing zip data type to character
code <- vroom::vroom(here::here("data","zip_code_database.csv"))
final_data <- left_join(CA_contributors, code, by = "zip")
final_hillary <- final_data %>%
filter(cand_nm == "Clinton, Hillary Rodham") %>%
group_by(cand_nm, primary_city) %>%
summarise(total_amt = sum(contb_receipt_amt)) %>%
slice_max(order_by = total_amt, n=10) %>% #derive top 10 cities
mutate(primary_city=fct_reorder(primary_city, total_amt)) %>% #reorder city by total amount
ggplot(
mapping=aes(x = total_amt, y=primary_city)) +
geom_col(fill="blue") +
scale_x_continuous(labels = scales::dollar_format()) +
labs(
title = "Clinton, Hillary Rodham"
)
final_trump <- final_data %>%
filter(cand_nm == "Trump, Donald J.") %>%
group_by(cand_nm, primary_city) %>%
summarise(total_amt = sum(contb_receipt_amt)) %>%
slice_max(order_by = total_amt, n=10) %>% #derive top 10 cities
mutate(primary_city=fct_reorder(primary_city, total_amt)) %>% #reorder city by total amount
ggplot(
mapping=aes(x = total_amt, y=primary_city)) +
geom_col(fill="red") +
scale_x_continuous(labels = scales::dollar_format()) + #x-axis is in $ units
labs(
title = "Trump, Donald J."
)
final_hillary + theme_bw(base_size = 10) + labs(x = "Amount Raised", y = "Primary City") +
final_trump + theme_bw(base_size = 10) + labs(x = "Amount Raised", y = "Primary City") #combine the two plots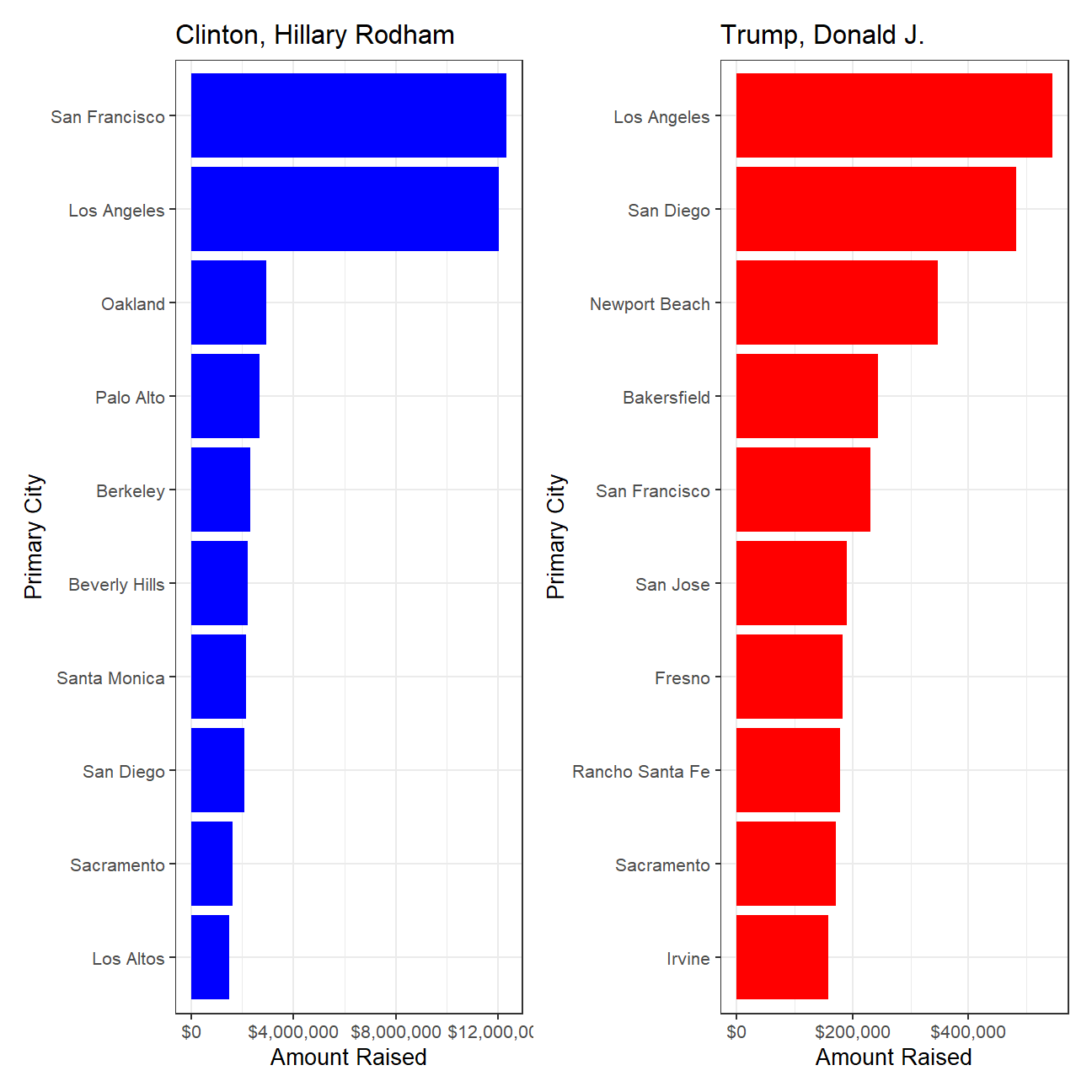
library(tidytext)
final_data## # A tibble: 1,292,843 × 19
## cand_nm contb…¹ zip contb_date type prima…² accep…³ unacc…⁴ state county
## <chr> <dbl> <chr> <date> <chr> <chr> <chr> <chr> <chr> <chr>
## 1 Clinton,… 50 94939 2016-04-26 STAN… Larksp… <NA> <NA> CA Marin…
## 2 Clinton,… 200 93428 2016-04-20 STAN… Cambria <NA> <NA> CA San L…
## 3 Clinton,… 5 92337 2016-04-02 STAN… Fontana <NA> <NA> CA San B…
## 4 Trump, D… 48.3 95334 2016-11-21 STAN… Living… <NA> <NA> CA Merce…
## 5 Sanders,… 40 93011 2016-03-04 PO B… Camari… <NA> <NA> CA Ventu…
## 6 Trump, D… 244. 95826 2016-11-24 STAN… Sacram… <NA> Walsh … CA Sacra…
## 7 Sanders,… 35 90278 2016-03-05 STAN… Redond… <NA> <NA> CA Los A…
## 8 Sanders,… 100 90278 2016-03-06 STAN… Redond… <NA> <NA> CA Los A…
## 9 Sanders,… 25 92084 2016-03-04 STAN… Vista <NA> <NA> CA San D…
## 10 Clinton,… 40 92637 2016-04-20 STAN… Laguna… Laguna… Laguna… CA Orang…
## # … with 1,292,833 more rows, 9 more variables: timezone <chr>,
## # area_codes <dbl>, latitude <dbl>, longitude <dbl>, world_region <chr>,
## # country <chr>, decommissioned <dbl>, estimated_population <dbl>,
## # notes <chr>, and abbreviated variable names ¹contb_receipt_amt,
## # ²primary_city, ³acceptable_cities, ⁴unacceptable_citiestop_ten <- final_data %>%
group_by(cand_nm) %>%
summarise(total_amt = sum(contb_receipt_amt)) %>%
slice_max(order_by = total_amt, n=10) #top 10 candidates
top_ten_vec <- c(top_ten) #create a vector for top 10 candidates
top_10_plot <- final_data %>%
filter(cand_nm == top_ten_vec$cand_nm) %>%
group_by(cand_nm, primary_city) %>%
summarise(total_amt = sum(contb_receipt_amt)) %>%
arrange(cand_nm,desc(total_amt)) %>% #order city by total amt for each candidate
top_n(10, total_amt) %>%
mutate(primary_city=reorder_within(primary_city, total_amt, cand_nm)) %>% #ordering within each candidate the top 10 cities by amount
ggplot(mapping=aes(x=total_amt, y=primary_city)) +
geom_col() +
facet_wrap(~cand_nm, scales = "free", ncol = 3) +
scale_y_reordered() +
theme_bw(base_size = 8.5) +
labs(
title = "Top 10 Cities for the Top Candidates",
x = "Year",
y = "City"
)
top_10_plot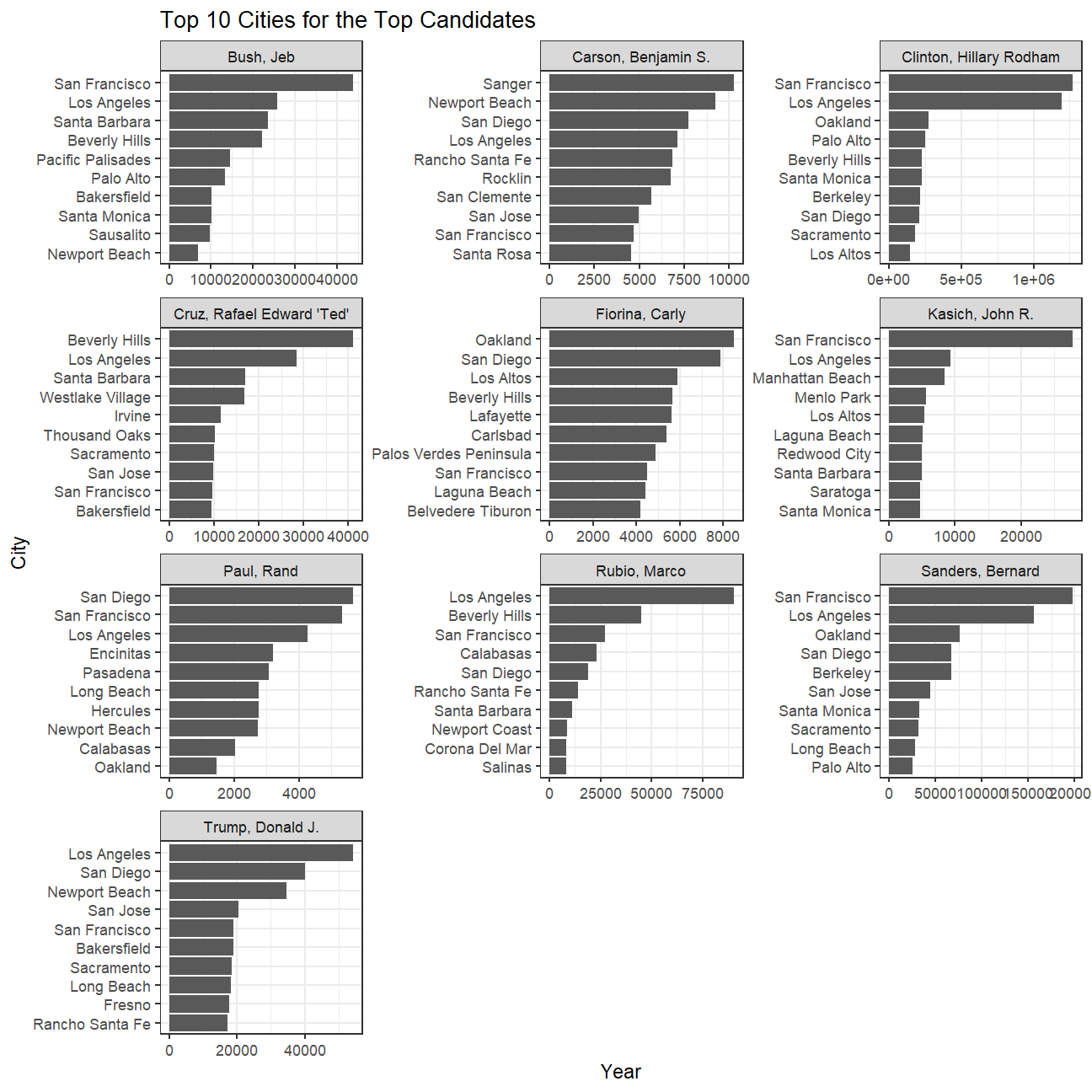
Details
- Who did you collaborate with: Group 6 - Sonakshi Gupta, Drishti Goyal, Jean Francois Peters, Wybe Harmes, Suzy Wang, Zezhou Tang
- Approximately how much time did you spend on this problem set: 7 hrs 30 min 20 sec
- What, if anything, gave you the most trouble: The challenge questions were tougher so we needed to use our best friends, “Google” and “StackR” to find the needed code, and hence, required some time.